Asynchronous execution

The Fibonacci sequence is a sequence of numbers starting with 0 and 1 where every subsequent number is the sum of the previous two numbers. In this example, we will use HPX to calculate the value of the n-th element of the Fibonacci sequence. In order to compute this problem in parallel, we will use a facility known as a future.

As shown in the Fig. 1 below, a future encapsulates a delayed computation. It acts as a proxy for a result initially not known, most of the time because the computation of the result has not completed yet. The future synchronizes the access of this value by optionally suspending any HPX-threads requesting the result until the value is available. When a future is created, it spawns a new HPX-thread (either remotely with a parcel or locally by placing it into the thread queue) which, when run, will execute the function associated with the future. The arguments of the function are bound when the future is created.

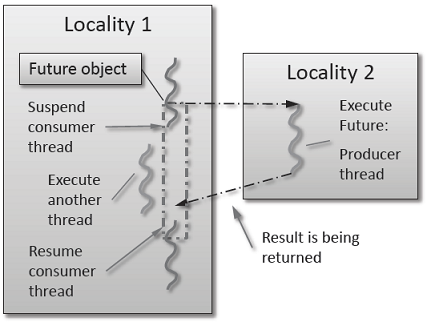
Fig. 1 Schematic of a future execution.

Once the function has finished executing, a write operation is performed on the future. The write operation marks the future as completed, and optionally stores data returned by the function. When the result of the delayed computation is needed, a read operation is performed on the future. If the future’s function hasn’t completed when a read operation is performed on it, the reader HPX-thread is suspended until the future is ready. The future facility allows HPX to schedule work early in a program so that when the function value is needed it will already be calculated and available. We use this property in our Fibonacci example below to enable its parallel execution.

Setup

The source code for this example can be found here: fibonacci_local.cpp.

To compile this program, go to your HPX build directory (see Building HPX for information on configuring and building HPX) and enter:

$ make examples.quickstart.fibonacci_local

To run the program type:

$ ./bin/fibonacci_local

This should print (time should be approximate):

fibonacci(10) == 55
elapsed time: 0.002430 [s]

This run used the default settings, which calculate the tenth element of the Fibonacci sequence. To declare which Fibonacci value you want to calculate, use the --n-value option. Additionally you can use the --hpx:threads option to declare how many OS-threads you wish to use when running the program. For instance, running:

$ ./bin/fibonacci --n-value 20 --hpx:threads 4

Will yield:

fibonacci(20) == 6765
elapsed time: 0.062854 [s]

Walkthrough

Now that you have compiled and run the code, let’s look at how the code works. Since this code is written in C++, we will begin with the main() function. Here you can see that in HPX, main() is only used to initialize the runtime system. It is important to note that application-specific command line options are defined here. HPX uses Boost.Program_options for command line processing. You can see that our programs --n-value option is set by calling the add_options() method on an instance of hpx::program_options::options_description. The default value of the variable is set to 10. This is why when we ran the program for the first time without using the --n-value option the program returned the 10th value of the Fibonacci sequence. The constructor argument of the description is the text that appears when a user uses the --hpx:help option to see what command line options are available. HPX_APPLICATION_STRING is a macro that expands to a string constant containing the name of the HPX application currently being compiled.

In HPX main() is used to initialize the runtime system and pass the command line arguments to the program. If you wish to add command line options to your program you would add them here using the instance of the Boost class options_description, and invoking the public member function .add_options() (see Boost Documentation for more details). hpx::init calls hpx_main() after setting up HPX, which is where the logic of our program is encoded.

int main(int argc, char* argv[])
{
    // Configure application-specific options
    hpx::program_options::options_description desc_commandline(
        "Usage: " HPX_APPLICATION_STRING " [options]");

    // clang-format off
    desc_commandline.add_options()
        ("n-value",
            hpx::program_options::value<std::uint64_t>()->default_value(10),
            "n value for the Fibonacci function")
        ;
    // clang-format on

    // Initialize and run HPX
    hpx::local::init_params init_args;
    init_args.desc_cmdline = desc_commandline;

    return hpx::local::init(hpx_main, argc, argv, init_args);
}

The hpx::init function in main() starts the runtime system, and invokes hpx_main() as the first HPX-thread. Below we can see that the basic program is simple. The command line option --n-value is read in, a timer (hpx::chrono::high_resolution_timer) is set up to record the time it takes to do the computation, the fibonacci function is invoked synchronously, and the answer is printed out.

int hpx_main(hpx::program_options::variables_map& vm)
{
    hpx::threads::add_scheduler_mode(
        hpx::threads::policies::scheduler_mode::fast_idle_mode);

    // extract command line argument, i.e. fib(N)
    std::uint64_t n = vm["n-value"].as<std::uint64_t>();

    {
        // Keep track of the time required to execute.
        hpx::chrono::high_resolution_timer t;

        std::uint64_t r = fibonacci(n);

        char const* fmt = "fibonacci({1}) == {2}\nelapsed time: {3} [s]\n";
        hpx::util::format_to(std::cout, fmt, n, r, t.elapsed());
    }

    return hpx::local::finalize();    // Handles HPX shutdown
}

The fibonacci function itself is synchronous as the work done inside is asynchronous. To understand what is happening we have to look inside the fibonacci function:

std::uint64_t fibonacci(std::uint64_t n)
{
    if (n < 2)
        return n;

    hpx::future<std::uint64_t> n1 = hpx::async(fibonacci, n - 1);
    std::uint64_t n2 = fibonacci(n - 2);

    return n1.get() + n2;    // wait for the Future to return their values
}

This block of code looks similar to regular C++ code. First, if (n < 2), meaning n is 0 or 1, then we return 0 or 1 (recall the first element of the Fibonacci sequence is 0 and the second is 1). If n is larger than 1 we spawn two new tasks whose results are contained in n1 and n2. This is done using hpx::async which takes as arguments a function (function pointer, object or lambda) and the arguments to the function. Instead of returning a std::uint64_t like fibonacci does, hpx::async returns a future of a std::uint64_t, i.e. hpx::future<std::uint64_t>. Each of these futures represents an asynchronous, recursive call to fibonacci. After we’ve created the futures, we wait for both of them to finish computing, we add them together, and return that value as our result. We get the values from the futures using the get method. The recursive call tree will continue until n is equal to 0 or 1, at which point the value can be returned because it is implicitly known. When this termination condition is reached, the futures can then be added up, producing the n-th value of the Fibonacci sequence.

Note that calling get potentially blocks the calling HPX-thread, and lets other HPX-threads run in the meantime. There are, however, more efficient ways of doing this. examples/quickstart/fibonacci_futures.cpp contains many more variations of locally computing the Fibonacci numbers, where each method makes different tradeoffs in where asynchrony and parallelism is applied. To get started, however, the method above is sufficient and optimizations can be applied once you are more familiar with HPX. The example Dataflow presents dataflow, which is a way to more efficiently chain together multiple tasks.